The DAV Maths Class 7 Solutions and DAV Class 7 Maths Chapter 9 Worksheet 1 Solutions of Construction of Triangles offer comprehensive answers to textbook questions.
DAV Class 7 Maths Ch 9 WS 1 Solutions
Question 1.
Fill in the blanks so as to make a true statement.
(i) Two line segments are congruent, if they have ________________ .
Answer:
the same length
(ii) Two angles are congruent, if they have ________________ .
Answer:
the same measurement
(iii) Two squares are congruent, if they have ________________ .
Answer:
the same length of sides
(iv) Two circles are congruent, if they have ________________ .
Answer:
the same radii
(v) Two rectangles are congruent, if they have ________________ .
Answer:
the same length and breadth.
![]()
Question 2.
In the given figure, state which pairs of triangles are congruent by SSS congruence condition. If congruent, write the congruence of triangles in symbolic form.

Answer:
In ∆ABC and ∆PQR,
AB = QR = 2 cm
BC = PR = 3 cm
AC = PQ = 2.5 cm
∴ ∆ABC ≅ ∆PQR [By SSS]
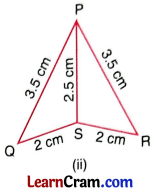
Answer:
In ∆ PQS and ∆ PRS
PQ = PR = 3.5 cm
QS = RS = 2 cm
PS = PS = 2.5 cm
∴ ∆PQS ≅ ∆ PRS [By SSS]

Answer:
In ∆ ABD and ∆ FEC
BD = CE = 3 cm
AD = CF = 5.5 cm
AB = EF = 3cm
∴ ∆ ABD ≅ ∆FEC [By SSS]

Answer:
In ∆ POQ and ∆ ROS
OQ = OS = 4cm
OP = OR = 3 cm
∠POQ = ∠ROS [Vertically opposite angles]
∴ ∆ POQ ≅ ∆ ROS [SAS]
Question 3.
In the given figure, PS = RS and PQ = RQ

(i) Is ∆ PQS ≅ ∆ RQS?
Answer:
PS = RS [given]
and PQ = RQ
SQ = SQ [Common]
∴ ∆ PQS ≅ ∆ RQS (By SSS)
(ii) State the three pairs of matching parts you have used to p answer (i).
Answer:
PS and RS, PQ and RQ and SQ = SQ
(iii) ∠P = ________________
Answer:
∠P = ∠R
![]()
Question 4.
In the given figure, ∆ ABC is isosceles with AB = AC. D is the mid-point of base BC.

(i) Is ∆ ADB = ∆ ADC? If yes, by which congruence condition?
Answer:
In ∆ ABD and ∆ ACD,
AB = AC
BD = DC
AD = AD
∆ ABD ≅ ∆ ACD
(ii) State the three pairs of matching parts that you use to arrive at your answer.
Answer:
AB and AC, BD and DC, AD and AD.
Question 5.
In ∆ PQR and ∆ XYZ, PQ = XZ and QR = YZ (See fig.). What additional information is required to make the two triangles congruent by SSS congruence condition?

Answer:
In ∆ PQR and ∆ XYZ,
PQ = XZ = 2.5 cm
QR = YZ = 4 cm
For SSS congruence condition we require third side PR = XY.
Question 6.
If ∆ ABC ≅ ∆ DEF, fill in the blanks to make each statement true.
(i) AB = ________________
(ii) ∠C = ________________
(iii) EF = ________________
(iv) ∠D = ________________
(v) CA = ________________
(vi) ∠B = ________________
Answer:

(i) DE
(ii) ∠F
(iii) BC
(iv) ∠A
(v) FD
(vi) ∠E
![]()
DAV Class 8 Maths Chapter 9 Worksheet 1 Notes
- Two figures are congruent, if they have exactly the same shape and size.
- Two lines are congruent, if they have the same length.
- Two angles are congruent, if they have the same measure.
- Two squares are congruent, if they have the same side length.
- Two rectangles are congruent, if they have the same length and same breadth.
- Two circles are congruent, if they have the same radii.
- Two triangles are said to be congruent if their corresponding parts are equal. The symbol of congruency is ’≅‘.
Example:
In ∆ABC and DEE, if AB = DE, BC = EF and AC = DF Also, ∠A = ∠D, ∠B = ∠E and ∠C = ∠F then ∆ ABC ≅ ∆ DEF.

Conditions of Congruency:
(i) If the sides of a triangle are equal to the corresponding sides of the other triangle, then the two triangles are congruent by (SSS) Fig. (i).
(ii) If any two sides and the angle included by them of a triangle are equal to any two sides and the angle included by them of other triangle, then the triangles are congruent by (SAS) Fig. (ii).
(iii) If any two angles and included side of one triangle are equal to any two angles and included side of the other triangle, then the triangles are congruent Fig. (iii).
(iv) In right triangles, if hypotenuse and one side of a triangle are equal to the hypotenuse and one side of other triangle, then the triangles are congruent by (RHS) Fig. (iv).

![]()
Example 1.
In the given figure, prove that the diagonal divides the rhombus ABCD info two congruent triangles.

Answer:
In ∆ ABD and ∆ CBD,
AB = BC [Sides of a rhombus are equal]
AD = DC
DB = DB [Common]
∴ ∆ABD ≅ ∆CBD [By SSS]
Example 2.
In the given figures, find ∠F, if ∆ ABC ≅ ∆ DEF.

Answer:
In ∆ ABC and ∆ DEF,
∆ ABC ≅ ∆ DEF
BC = DF =4 cm
AC = EF = 5 cm
∴ ∠F = ∠C = 30° [Included angles]
Hence ∠F = 30°.
Example 3.
In the given figure, prove that ∆ ABC ≅ ∆ DBC.

Answer:
In ∆ ABC and ∆ DBC,
BC = BC
∠ACB = ∠DBC = 30° [Common]
∠ABC = ∠DCB
= 40° + 30° = 70°
∴ ∆ ABC ≅ ∆ DBC [By ASA]
![]()
Example 4.
In the given figure, prove that ∆ ABC ≅ ∆ DEF.

Answer:
In ∆ ABC and ∆ DEF,
AC = DF = 13 cm
AB = EF = 8 cm
∠B = ∠E = 90°
∴ ∆ ABC ≅ ∆ DEF [By RHS].