Free PDF Download of CBSE Class 10 Maths Chapter 9 Application of Trigonometry Multiple Choice Questions with Answers. MCQ Questions for Class 10 Maths with Answers was Prepared Based on Latest Exam Pattern. Students can solve NCERT Class 10 Maths Application of Trigonometry MCQs with Answers to know their preparation level.
Class 10 Maths MCQs Chapter 9 Application of Trigonometry
MCQ On Application Of Trigonometry Class 10 Question 1. The shadow of a tower is equal to its height at 10-45 a.m. The sun’s altitude is
(a) 30°
(b) 45°
(c) 60°
(d) 90°
Answer/ Explanation
Answer: b
Explaination: Reason: Let the height of tower BC = rm and sun’s altitude = θ
Then Length of its shadow, AB = x m

In rt. ∆ABC, tan θ = \(\frac{BC}{AB}\) = \(\frac{x}{x}\) = 1
⇒ tan θ = tan 450
∴ θ = 45°
2. In given figure, the value of CE is

(a) 12 cm
(b) 6 cm
(c) 9 cm
(d) 6√3 cm
Answer/ Explanation
Answer: a
Explaination: Reason: In rt. ∆EBC, cos 60° = \(\frac{BC}{CE}\)
⇒ \(\frac{1}{2}\) = \(\frac{6}{CE}\)
⇒ CE = 12 cm
MCQ Questions For Class 10 Maths Trigonometry Question 3. In given figure, the value of ZC is
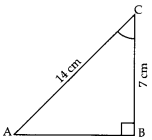
(a) 90°
(b) 45°
(c) 30°
(d) 60°
Answer/ Explanation
Answer: d
Explaination: Reason: In rt. ∆ABC, cos C = \(\frac{BC}{AB}\) = \(\frac{7}{14}\) = \(\frac{1}{2}\)
⇒ cos C = cos 60°
∴ C = 60°
MCQ On Application Of Trigonometry Question 4. In given Fig., the angle of depression from the observing position D and E of the object at A are
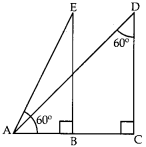
(a) 60°, 60°
(b) 30°, 30°
(c) 30°, 60°
(d) 60°, 30°
Answer/ Explanation
Answer: c
Explaination:

Reason: ∵ APD, ∠1 = 90° – 60° = 30°
∴ APE, ∠2 = ∠EAB …[alt Zs]
∴ ∠2 = 60°
Hence the angles of depression at D and E are 30° and 60° respectively.
Some Applications Of Trigonometry Class 10 MCQ Question 5. In given figure, the length of AP is

Answer/ Explanation
Answer: b
Explaination:

MCQ NCERT Application Of Trigonometry Class 10 Question 6. In given figure, the value of AE is

Answer/ Explanation
Answer: a
Explaination: Reason: ∠AED = ∠EAB = 30°

In rt. ∆AED, sin 30° = \(\frac{AD}{AP}\)
⇒ \(\frac{1}{2}\) = \(\frac{45}{AE}\)
⇒ AE = 90 cm
Trigonometry MCQ Class 10 Question 7. In given figure, AD = 4 cm, BD = 3 cm and CB = 12 cm. The value of tan θ is
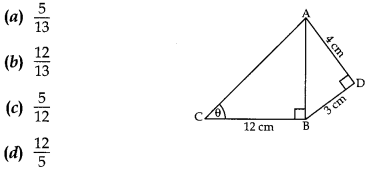
Answer/ Explanation
Answer: c
Explaination: Reason: In rt ∆ADB,
AB² = AD² + BD² = (4)² + (3)² = 16 + 9 = 25
∴ AB = √25 = 5
∴ In rt ∆ABC, tan θ \(\frac{AB}{BC}\) = \(\frac{5}{12}\)
8. In figure given ABCD is a rectangle, the value of CE is

(a) 1 cm
(b) 2 cm
(c) 3 cm
(d) 4 cm
Answer/ Explanation
Answer: d
Explaination: Reason: Since ABCD is a rectangle
∴ BC = AD = 8 cm and B = 90°
In rt ∆CBE, cos 60° = \(\frac{CE}{BC}\)
⇒ \(\frac{1}{2}\) = \(\frac{CE}{8}\)
∴ CE = \(\frac{8}{2}\) = 4 cm
Trigonometry MCQ Questions Question 9. In given figure, ABCD is a || gm. The lenght of AP is

(a) 2 cm
(b) 4 cm
(c) 6 cm
(d) 8 cm
Answer/ Explanation
Answer: c
Explaination: Reason: Since ABCD is a || gm
∴ AD = BC = 4√3
In rt ∆APD, sin 60° = \(\frac{AP}{AD}\)
⇒ \(\frac{\sqrt{3}}{2}=\frac{\mathrm{AP}}{4 \sqrt{3}}\)
⇒ 2AP = 4 × 3 = 12
∴ AP = 6 cm
MCQ On Trigonometry For Class 10 With Solutions Question 10. When the length of shadow of a vertical pole is equal to √3 times of its height, the angle of elevation of the Sun’s altitude is
(a) 30°
(b) 45°
(c) 60°
(d) 15°
Answer/ Explanation
Answer: a
Explaination: Reason: Let the height of the vertical pole, BC = h m
∴ Shadow AB = √3 h m and the angle of elevation ZBAC = θ

In rt ∆ABC, tan θ = \(\frac{B C}{A B}=\frac{h}{\sqrt{3} h}=\frac{1}{\sqrt{3}}\) = tan 30°
∴ θ = 30°
Hence the Sun’s altitude is 30°
MCQ Trigonometry Class 10 Question 11. The angle of elevation of top of a tower from a point on the ground, which is 30 m away from the foot of the tower is 30°. The length of the tower is
(a) √3 m
(b) 2√3 m
(c) 5√3m
(d) 10√3 m
Answer/ Explanation
Answer: d
Explaination:
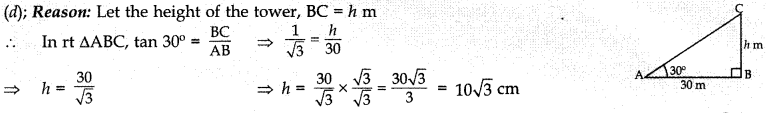
MCQ Questions On Trigonometry For Class 10 Question 12. A plane is observed to be approaching the airport. It is at a distance of 12 km from the point of observation and makes an angle of elevation of 60°. The height above the ground of the plane is
(a) 6√3 m
(b) 4√3 m
(c) 3√3 m
(d) 2√3 m
Answer/ Explanation
Answer: a
Explaination:

Trigonometry Multiple Choice Questions And Answers Pdf Question 13. The upper part of a tree is broken by the wind and makes an angle of 30° with the ground. The distance from the foot of the tree to the point where the top touches the ground is 5 m. The height of the tree is
(a) 10√33 m
(b) 5√33 m
(c) √3 m
(d) √3/5 m
Answer/ Explanation
Answer: b
Explaination:

MCQ On Trigonometry 10th Question 14. The angles of elevation of the top of a rock from the top and foot of 100 m high tower are respectively 30° and 45°. The height of the rock is
(a) 50 m
(b) 150 m
(c) 5o√3m
(d) 50(3 + √3)
Answer
Answer: d
Trigonometry MCQs Question 15. The tops of two poles of height 20 m and 14 m are connected by a wire. If the wire makes an angle of 30° with horizontal, the length of the wire is
(a) 6 m
(b) 10 m
(c) 12 m
(d) 20 m
Answer
Answer: c
We hope the given MCQ Questions for Class 10 Maths Application of Trigonometry with Answers will help you. If you have any query regarding CBSE Class 10 Maths Chapter 9 Application of Trigonometry Multiple Choice Questions with Answers, drop a comment below and we will get back to you at the earliest.