DAV Class 7 Maths Chapter 9 Worksheet 3 Solutions

The DAV Maths Class 7 Solutions and DAV Class 7 Maths Chapter 9 Worksheet 3 Solutions of Construction of Triangles offer comprehensive answers to textbook questions.

DAV Class 7 Maths Ch 9 WS 3 Solutions

Question 1.
In the given figure, ∠P = ∠Y = 40° and ∠Q = ∠Z = 60°. Find the third pair of corresponding parts which make ∆PQR ≅ ∆YZX, by ASA congruence condition.
DAV Class 7 Maths Chapter 9 Worksheet 3 Solutions 1
Answer:
∠P = ∠Y = 40° (given)
∠Q = ∠Z = 60° (given)
And Third pair of corresponding part is
PQ = ZY
∆PQR ≅ ∆YZX (By SAS)

Question 2.
Which pairs of triangles are congruent by ASA congruence condition in the given figure? If congruent, write the congruence of the two triangles in symbolic form.
DAV Class 7 Maths Chapter 9 Worksheet 3 Solutions 2
Answer:
In ∆ABC and ∆ ZXY,
∠C = ∠Y = 60° (given)
∠A = ∠Z = 40° (given)
AC = YZ = 3.5 cm (given)
∆ABC ≅ ∆ZXY (By ASA)

DAV Class 7 Maths Chapter 9 Worksheet 3 Solutions 3
Answer:
In ∆ABO and ∆CDO,
∠ABO = ∠CDO = 80°
BO = OD = 4 cm
∠AOB = ∠COD
∆ABO ≅ ∆CDO

DAV Class 7 Maths Chapter 9 Worksheet 3 Solutions 4
Answer:
In ∆ABC and ∆DCB,
∠ABC = ∠DCB
= 40° + 20°
= 60°
∠ACB = ∠DBC = 40°
BC = BC
∆ABC ≅ ∆ DCB

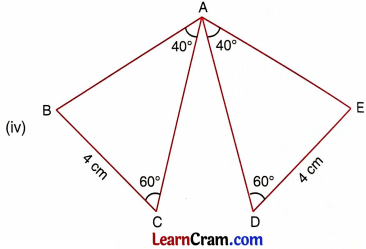
DAV Class 7 Maths Chapter 9 Worksheet 3 Solutions 5
Answer:
In ∆ABC and ∆AED,
∠B = ∠E = 180° – (40° + 60°)
= 80°
∠C = ∠D = 60°
BC = DE = 4 cm
∆ ABC ≅ ∆ AED

DAV Class 7 Maths Chapter 9 Worksheet 3 Solutions 6
Answer:
In ∆ABC and ∆ XZY,
No side of ∆ABC is given equal to the corresponding
Hence they are not congruent by ASA

Question 3.
In the given figure, QX bisects ∠PQR as well as ∠PSR.
State the three facts needed to ensure that ∆QRS ≅ ∆QPS.
Give reasons for each statement.
DAV Class 7 Maths Chapter 9 Worksheet 3 Solutions 7
Answer:
In ∆QRS and ∆QPS,
∠PQS = ∠RQS (given)
∠PSQ = ∠RSQ (given)
QS = QS
∆QRS ≅ ∆QPS

Question 4.
In the given figure, PS bisects ∠P and PS ± QR.
DAV Class 7 Maths Chapter 9 Worksheet 3 Solutions 8
(i) Is ∆PSQ ≅ ∆PSR?
Answer:
In ∆PQS and ∆PRS,
∠QPS = ∠RPS (given)
∠PSQ = ∠PSR = 90° (given)
PS = PS (Common)
∆PSQ ≅ ∆PSR (ASA)

(ii) State the three pairs of matching parts you have used in (i)
Answer:
∠QPS and ∠RPS, ∠PSQ and ∠PSR, PS and PS

(iii) Is it true to say that QS = SR? Why?
Answer:
Yes, QS = SR [Corresponding parts of congruent triangles]

Question 5.
In the given figure, AO = BO and ∠A = ∠B
DAV Class 7 Maths Chapter 9 Worksheet 3 Solutions 9
(i) Is ∠AOC = ∠BOD ? Why?
(ii) Is ∆AOC ≅ ∆BOD by ASA congruence condition ?
(iii) State the three facts you have used to answer (ii)
(iv) Is ∠ACO = ∠BDO? Why?
Answer:
In ∆AOC and ∆BOD
AO = BO (given)
∠A= ∠B (given)
(i) ∠AOC = ∠BOD
(ii) ∴ ∆ AOC ≅ ∆ BOD
(iii) AO and BO, ∠A and ∠B, ∠AOC and ∠BOD
(iv) ∠ACO = ∠BDO (Corresponding parts of congruent triangles)