DAV Class 5 Maths Chapter 3 Worksheet 9 Solutions

The DAV Class 5 Maths Book Solutions Pdf and DAV Class 5 Maths Chapter 3 Worksheet 9 Solutions of Multiples and Factors offer comprehensive answers to textbook questions.

DAV Class 5 Maths Ch 3 Worksheet 9 Solutions

Question 1.
Fill in the blanks.
(a) Factorisation of 16 is _______

Solution:
Prime factorisation of 16 is 2 × 2 × 2 × 2

(b) Factorisation of 30 is _________

Solution:
Prime factorisation of 30 is 2 × 3 × 5

(c) Prime factorisation of 70 is _______

Solution:
Prime factorisation of 70 is 2 × 5 × 7

Question 2.
Using the Factor Tree Method, find the prime factorisation of the following:
(a) 8
Solution:
Prime factorisation of 8 = 2 × 2 × 2

(b) 20
Solution:
Prime factorisation of 20 = 2 × 2 × 5

(c) 34
Solution:
Prime factorisation of 34 = 2 × 17

(d) 44
Solution:
Prime factorisation of 44 = 2 × 2 × 11

(e) 21
Solution:
Prime factorisation of 21 = 3 × 7

(f) 42
Solution:
Prime factorisation of 42 = 2 × 3 × 7

(g) 38
Solution:
Prime factorisation of 38 = 2 × 19

(h) 45
Solution:
Prime factorisation of 45 = 3 × 3 × 5

Question 3.
Using the Division Method, find the prime factorisation of the following:
(a) 27
Solution:
Prime factorisation of 27 = 3 × 3 × 3

(b) 34
Solution:
Prime factorisation of 34 = 2 × 17

(c) 92
Solution:
Prime factorisation of 92 = 2 × 2 × 23

(d) 48
Solution:
Prime factorisation of 48 = 2 × 2 × 2 × 2 × 3

(e) 64
Solution:
Prime factorisation of 64 = 2 × 2 × 2 × 2 × 2 × 2

(f) 45
Solution:
Prime factorisation of 45 = 3 × 3 × 5

(g) 72
Solution:
Prime factorisation of 72 = 2 × 2 × 2 × 3 × 3

(h) 99
Solution:
Prime factorisation of 99 = 3 × 3 × 11

Question 4.
Fill in the missing numbers.

Solution:

Solution:

Solution:

Solution:

Solution:

DAV Class 5 Maths Chapter 3 Worksheet 9 Notes

Factor Tree Method:
We take the composite number 20.

We break 20 into two factors i.e., 2 and 10. Here 2 is prime but 10 is composite. We again break 10 into two prime factors i.e., 2 and 5. The prime factorisation of 20 is 2 × 2 × 5.
A prime factorisation will contain no composite number.

Division Method:
Take the composite number 48 and divide it by the smallest possible prime number.


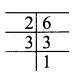
Divide 48 by prime number 2 and write quotient (24) below
Divide 24 by prime number 2
Divide 12 by prime number 2
Divide 6 by prime number 2
Divide 3 by prime number 3
Stop when you get 1.
We start dividing by the smallest possible prime number and keep on doing the same, till we get 1.