Maharashtra state Board 10th Standard Solutions Chapter 1 Linear Equations in two Variables – Here are all the MH Board solutions for 10th Standard maths Practice Set 1.5. This solution contains questions, answers, images, explanations of the complete Practice Set 1.5 titled Linear Equations in two Variables of maths taught in 10th Standard. If you are a student of 10th Standard who is using Maharashtra state Board Textbook to study maths, then you must come across Practice Set 1.5 Linear Equations in two Variables. After you have studied lesson, you must be looking for answers of its questions. Here you can get complete Maharashtra Board Solutions for 10th Standard maths Chapter 1 Linear Equations in two Variables in one place.
Maharashtra State Board Class 10 Maths Solutions Chapter 1 Linear Equations in Two Variables Practice Set 1.5
Question 1.
Two numbers differ by 3. The sum of twice the smaller number and thrice the greater number is 19. Find the numbers.
Solution:
Let the greater number be x and the smaller number be y.
According to the first condition, x – y = 3 …(i)
According to the second condition,
3x + 2y = 19 …(ii)
Multiplying equation (i) by 2, we get
2x – 2y = 6 …(iii)
Adding equations (ii) and (iii), we get
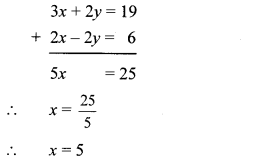
Substituting x = 5 in equation (i), we get
5 – y = 3
∴ 5 – 3 = y
∴ y = 2
∴ The required numbers are 5 and 2.
Question 2.
Complete the following.

Solution:
Opposite sides of a rectangle are equal.
∴ 2x + y + 8 = 4x – y
∴ 8 = 4x – 2x – y – y
∴ 2x – 2y = 8
∴ x – y = 4 …(i)[Dividingboth sides by 2]
Also, x + 4= 2y
∴ x – 2y = -4 …(ii)
Subtracting equation (ii) from (i), we get

Substituting y = 8 in equation (i), we get
x – 8 = 4
∴ x = 4 + 8
∴ x = 12
Now, length of rectangle = 4x – y
= 4(12) – 8
= 48 – 8
∴ Length of rectangle = 40
Breadth of rectangle = 2y = 2(8) = 16
Perimeter of rectangle = 2(length + breadth)
= 2(40 + 16)
= 2(56)
∴ Perimeter of rectangle =112 units
Area of rectangle = length × breadth
= 40 × 16
∴ Area of rectangle = 640 sq. units
∴ x = 12 and y = 8, Perimeter of rectangle is 112 units and area of rectangle is 640 sq. units.
Question 3.
The sum of father’s age and twice the age of his son is 70. If we double the age of the father and add it to the age of his son the sum is 95. Find their present ages.
Solution:
Let the present ages of father and son be x years and y years respectively.
According to the first condition,
x + 2y = 70 …(i)
According to the second condition,
2x + y = 95 …(ii)
Multiplying equation (i) by 2, we get
2x + 4y = 140 …(iii)
Subtracting equation (ii) from (iii), we get

Substituting y = 15 in equation (i), we get
x + 2(15) = 7O
⇒ x + 30 = 70
⇒ x = 70 – 30
∴ x = 40
∴ The present ages of father and son are 40 years and 15 years respectively.
Question 4.
The denominator of a fraction is 4 more than twice its numerator. Denominator becomes 12 times the numerator, if both the numerator and the denominator are reduced by 6. Find the fraction.
Solution:
Let the numerator of the fraction be x and the denominator be y.
∴ Fraction = \(\frac { x }{ y } \)
According to the first condition,
y = 2x + 4
∴ 2x – y = -4 …(i)
According to the second condition,
(y – 6)= 12(x – 6)
∴ y – 6 = 12x – 72
∴ 12x – y = 72 – 6
∴ 12x – y = 66 …(ii)
Subtracting equation (i) from (ii), we get
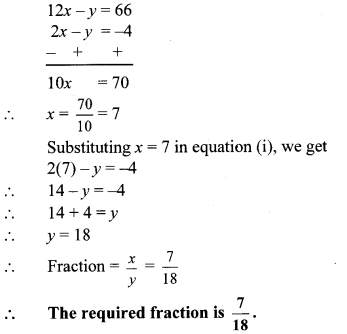
Question 5.
Two types of boxes A, B ,are to be placed in a truck having capacity of 10 tons. When 150 boxes of type A and 100 boxes of type B are loaded in the truck, it weights 10 tons. But when 260 boxes of type A are loaded in the truck, it can still accommodate 40 boxes of type B, so that it is fully loaded. Find the weight of each type of box.
Solution:
Let the weights of box of type A be x kg and that of box of type B be y kg.
1 ton = 1000 kg
∴ 10 tons = 10000 kg
According to the first condition,
150x + 100y = 10000
∴ 3x + 2y = 200 …(i) [Dividing both sides by 50]
According to the second condition,
260x + 40y = 10000
∴ 13x + 2y = 500 …(ii) [Dividing both sides by 20]
Subtracting equation (i) from (ii), we get

∴ The weights of box of type A is 30 kg and that of box of type B is 55 kg.
Question 6.
Out of 1900 km, Vishal travelled some distance by bus and some by aeroplane. Bus travels with average speed 60 km/hr and the average speed of aeroplane is 700 km/hr. It takes 5 hours to complete the journey. Find the distance Vishal travelled by bus.
Solution:
Let the distance Vishal travelled by bus be x km and by aeroplane be y km.
According to the first condition,
x + y = 1900 …(i)
\(\text { Time }=\frac{\text { Distance }}{\text { Speed }} \)
∴ Time required to cover x km by bus = \(\frac { x }{ 60 } \) hr
Time required to cover y km by aeroplane
= \(\frac { y }{ 700 } \) hr
According to the second condition,

Multiplying equation (i) by 6, we get
6x + 6y= 11400 …(iii)
Subtracting equation (iii) from (ii), we get

∴ The distance Vishal travelled by bus is 150 km.
Question 1.
There are some instructions given below. Frame the equations from the information and write them in the blank boxes shown by arrows. (Textbook pg. no. 20)
Answer:
