Maharashtra state Board 10th Standard Solutions Chapter 1 Linear Equations in two Variables – Here are all the MH Board solutions for 10th Standard maths Practice Set 1.1. This solution contains questions, answers, images, explanations of the complete Practice Set 1.1 titled Linear Equations in two Variables of maths taught in 10th Standard. If you are a student of 10th Standard who is using Maharashtra state Board Textbook to study maths, then you must come across Practice Set 1.1 Linear Equations in two Variables. After you have studied lesson, you must be looking for answers of its questions. Here you can get complete Maharashtra Board Solutions for 10th Standard maths Chapter 1 Linear Equations in two Variables in one place.
Maharashtra State Board Class 10 Maths Solutions Chapter 1 Linear Equations in Two Variables Practice Set 1.1
Question 1.
Complete the following activity to solve the simultaneous equations.
5x + 3y = 9 …(i)
2x-3y=12 …(ii)
Solution:
5x + 3y = 9 …(i)
2x-3y=12 …(ii)
Add equations (i) and (ii).

Question 2.
Solve the following simultaneous equations.
i. 3a + 5b = 26; a + 5b = 22
ii. x + 7y = 10; 3x – 2y = 7
iii. 2x – 3y = 9; 2x + y = 13
iv. 5m – 3n = 19; m – 6n = -7
v. 5x + 2y = -3;x + 5y = 4
vi. \(\frac { 1 }{ 3 } \) x+ y = \(\frac { 10 }{ 3 } \) ; 2x + \(\frac { 1 }{ 4 } \) y = \(\frac { 11 }{ 4 } \)
vii. 99x + 101y = 499 ; 101x + 99y = 501
viii. 49x – 57y = 172; 57x – 49y = 252
Solution:
i. 3a + 5b = 26 …(i)
a + 5b = 22 …(ii)
Subtracting equation (ii) from (i), we get

Substituting a = 2 in equation (ii), we get
2 + 5b = 22
∴ 5b = 22 – 2
∴ 5b = 20
∴ b = \(\frac { 20 }{ 5 } \) =4
∴ (a, b) = (2, 4) is the solution of the given simultaneous equations.
ii. x + 7y = 10
∴ x = 10 – 7y …(i)
3x – 2y = 7 …1(ii)
Substituting x = 10 – ly in equation (ii), we get
3 (10 – 7y) – 2y = 7
∴ 30 – 21y – 2y = 7
∴ -23y = 7 – 30
∴ -23y = -23
∴ y = \(\frac { -23 }{ -23 } \)
Substituting y = 1 in equation (i), we get
x = 10 – 7 (1)
= 10 – 7 = 3
∴ (x, y) = (3, 1) is the solution of the given simultaneous equations.
iii. 2x – 3y = 9 …(i)
2x + y = 13 …(ii)
Subtracting equation (ii) from (i), we get
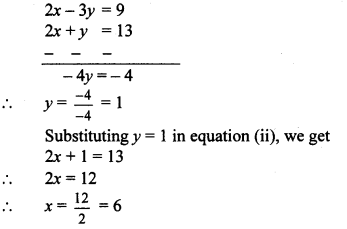
∴ (x, y) = (6, 1) is the solution of the given simultaneous equations.
iv. 5m – 3n = 19 …(i)
m – 6n = -7
∴ m = 6n – 7 …(ii)
Substituting m = 6n – 7 in equation (i), we get
5(6n – 7) – 3n = 19
∴ 30n – 35 – 3n = 19
∴ 27n = 19 + 35
∴ 27n = 54
∴ n = \(\frac { 54 }{ 27 } \) = 2
Substituting n = 2 in equation (ii), we get
m = 6(2) – 7
= 12 – 7 = 5
∴ (m, n) = (5, 2) is the solution of the given simultaneous equations.
v. 5x + 2y = -3 …(i)
x + 5y = 4
∴ x = 4 – 5y …(ii)
Substituting x = 4 – 5y in equation (i), we get
5(4 – 5y) + 2y = -3
∴ 20 – 25y + 2y = -3
∴ -23y = -3 – 20
∴ -23y = -23
∴ y = \(\frac { -23 }{ -23 } \) = 1
Substituting y = 1 in equation (ii), we get
x = 4 – 5(1)
= 4 – 5 = -1
∴ (x, y) = (-1, 1) is the solution of the given simultaneous equations.

Substituting y = 3 in equation (i), we get
x = 10 – 3(3)
= 10 – 9 = 1
∴ (x, y) = (1, 3) is the solution of the given simultaneous equations.
vii. 99x + 101 y = 499 …(i)
101 x + 99y = 501 …(ii)
Adding equations (i) and (ii), we get

Substituting x = 3 in equation (iii), we get
3 + y = 5
∴ y = 5 – 3 = 2
∴ (x, y) = (3, 2) is the solution of the given simultaneous equations.
viii. 49x – 57y = 172 …(i)
57x – 49y = 252 …(ii)
Adding equations (i) and (ii), we get

Substituting x = 7 in equation (iv), we get
7 + y = 10
∴ y = 10 – 7 = 3
∴ (x, y) = (7, 3) is the solution of the given simultaneous equations.
Complete the following table. (Textbook pg. no. 1)

Question 1.
Solve: 3x+ 2y = 29; 5x – y = 18 (Textbook pg. no. 3)
Solution:
3x + 2y = 29 …(i)
and 5x- y = 18 …(ii)
Let’s solve the equations by eliminating ‘y’.
Fill suitably the boxes below.
Multiplying equation (ii) by 2, we get
