Free PDF Download of CBSE Class 10 Maths Chapter 10 Circles Multiple Choice Questions with Answers. MCQ Questions for Class 10 Maths with Answers was Prepared Based on Latest Exam Pattern. Students can solve NCERT Class 10 Maths Circles MCQs with Answers to know their preparation level.
Class 10 Maths MCQs Chapter 10 Circles
Circle Multiple Choice Question 1. The distance between two parallel tangents of acircle of radius 4 cm is
(a) 2 cm
(b) 4 cm
(c) 6 cm
(d) 8 cm
Answer/ Explanation
Answer: d
Explaination:

Reason: Here radius, r = 4 cm
Required distance,
AB = OA + OB
= r + r = 2r = 2×4 = 8 cm
2. In the given figure, if ZRPS = 25°, the value of ZROS is

(a) 135°
(b) 145°
(c) 165°
(d) 155°
Answer/ Explanation
Circles Class 10 MCQ With Answer: dExplaination: Reason: Since OR ⊥ PR and OS ⊥ PS
∴ ∠ORP = ∠OSP = 90°
In □ ORPS, ∠ROS + ∠ORP + ∠RPS + ∠OSP = 360°
∠ROS + 90° + 25° + 90° = 360°
∠ROS = 360° – 205° = 155°
3. A tangent is drawn from a point at a distance of 17 cm of circle C(0, r) of radius 8 cm. The length of its tangent is
(a) 5 cm
(b) 9 cm
(c) 15 cm
(d) 23 cm
Answer/ Explanation
Answer: c
Explaination:

Reason: In rt ∆OAP, AP² + OA² = OP²
⇒ AP² + (8)² = (17)² => AP² + 64 = 289
⇒ AP² = 289 – 64 = 225
∴ AP = √225 = 15 cm
4. The length of tangents drawn from an external point to the circle
(a) are equal
(b) are not equal
(c) sometimes are equal
(d) are not defined
Answer/ Explanation
Answer: a
Explaination: Reason: Since the length of tangents drawn from an external point to a circle are equal.
5. Number of tangents drawn at a point of the , circle is/are
(a) one
(b) two
(c) none
(d) infinite
Answer/ Explanation
Answer: a
Explaination: Reason: There is only one tangent at a point of the circle.
6. The tangents drawn at the extremities of the diameter of a circle are
(a) perpendicular
(b) parallel
(c) equal
(d) none of these
Answer/ Explanation
Answer: b
Explaination:

Reason: Since OP ⊥ AB and OQ ⊥ CD
∴ Z1 = 90° and Z2 = 90°
⇒ ∠1 = Z2, which are alternate angles.
∴ AB || CD
7. Tangents from an external point to a circle are
(a) equal
(b) not equal
(c) parallel
(d) perpendicular
Answer/ Explanation
MCQs of Maths for Class 10 With Answer: aExplaination: Reason: Tangents from external points to a circle are equal.
8. The length of a tangent drawn from a point at a distance of 10 cm of circle is 8 cm. The radius of the circle is
(a) 4 cm
(b) 5 cm
(c) 6 cm
(d) 7 cm
Answer/ Explanation
Answer: c
Explaination:
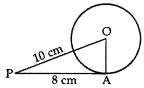
Reason: In rt. AOAP, we have
OA² + AP² = OP²
⇒ OA² + (8)² = (10)2
⇒ OA² + 64 = 100
⇒ OA² = 100 – 64 = 36
∴ OA = √36 = 6 cm
MCQ Questions on Circles for Class 10 Question 9. In given figure, CP and CQ are tangents to a circle with centre O. ARB is another tangent touching the circle at R. If CP = 11 cm and BC = 6 cm then the length of BR is
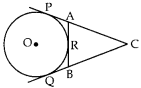
(a) 6 cm
(b) 5 cm
(c) 4 cm
(d) 3 cm
Answer/ Explanation
Answer: b
Explaination: Reason: Since
BQ = BR …(i) [∵ Tangents drawn from external points are equal]
CQ = CP …[Using (i)]
BC + BQ = 11
⇒ 6 + BR = 11
⇒ BR = 11 – 6 = 5 cm
10. From a point P which is at a distance of 13 cm from the centre O of a circle of radius 5 cm, the pair of tangents PQ and PR to the circle are drawn. Then the area of the quadrilateral PQOR is
(a) 60 cm²
(b) 65 cm²
(c) 30 cm²
(d) 32.5 cm²
Answer/ Explanation
Answer: a
Explaination:

Reason: OP² = OQ² + PQ²
169 = 25 + PQ²
PQ² = 144
PQ = 12
Area PQOR = ar (AOPQ) + ar (AOPR)
= \(\frac{1}{2}\) × 12 × 5 + \(\frac{1}{2}\) × 12 × 5 = 60 cm²
We hope the given MCQ Questions for Class 10 Maths Circles with Answers will help you. If you have any query regarding CBSE Class 10 Maths Chapter 10 Circles Multiple Choice Questions with Answers, drop a comment below and we will get back to you at the earliest.